
Zadanie Tramwaj (tra)
Pomóż nam usprawnić bazę zadań!
Tram
Memory limit: 64 MB
Byteman has looked out of the window and seen an old tram at the stop in front of his house. He tried to make a photo of it to add to his collection of old vehicles' photos, but the tram had gone before he reached for his camera.
Byteman lives in Bytetown.
There are  junctions in the town numbered from
junctions in the town numbered from 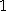 to
to  and near each junction there is a tram stop.
Public transport is very punctual there and the trams arrive at stops exactly at full minutes.
Hence, he decided to look out of the window every minute, hoping that the unique tram will appear at the stop again.
After a while it became annoying and Byteman decided to look for a smarter solution.
He took a map of Bytetown and started analysing it (which was not easy, as he looked out of the window every minute).
Eventually, he set the camera to make a photo of the stop every
and near each junction there is a tram stop.
Public transport is very punctual there and the trams arrive at stops exactly at full minutes.
Hence, he decided to look out of the window every minute, hoping that the unique tram will appear at the stop again.
After a while it became annoying and Byteman decided to look for a smarter solution.
He took a map of Bytetown and started analysing it (which was not easy, as he looked out of the window every minute).
Eventually, he set the camera to make a photo of the stop every 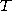 minutes.
He chose the number
minutes.
He chose the number 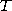 as the largest such integer that a camera making photos
of the stop every
as the largest such integer that a camera making photos
of the stop every 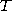 minutes, starting from the first appearance of the old tram, will
not miss any arrival of the tram at the stop, regardless of the route it takes.
minutes, starting from the first appearance of the old tram, will
not miss any arrival of the tram at the stop, regardless of the route it takes.
The result was so interesting for Byteman, that he started thinking what result (let us denote it by 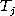 )
would he obtain, if he lived next to a different,
)
would he obtain, if he lived next to a different, 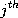 , tram stop.
Thus
, tram stop.
Thus 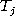 is the largest integer such that if Byteman lived next to the
is the largest integer such that if Byteman lived next to the 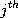 junction
and the tram appeared at the stop at minute 0, then, regardless
of its route, all its following appearances at the stop would occur in minutes
which are multiples of
junction
and the tram appeared at the stop at minute 0, then, regardless
of its route, all its following appearances at the stop would occur in minutes
which are multiples of 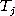 .
If no track begins at the
.
If no track begins at the 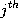 junction or a tram that leaves the junction never returns,
junction or a tram that leaves the junction never returns, 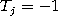 .
.
Input
In the first line of the standard input there are two integers  and
and 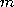 (
(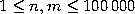 ), separated by a single space, representing the number
of junctions in the town and the number of connections between them.
The junctions are numbered from
), separated by a single space, representing the number
of junctions in the town and the number of connections between them.
The junctions are numbered from 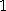 to
to  .
In the following
.
In the following 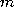 lines there is a description of the tram network in Bytetown.
The
lines there is a description of the tram network in Bytetown.
The 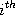 of those lines contains three integers
of those lines contains three integers 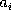 ,
, 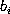 ,
, 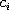 (
(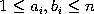 ,
, 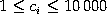 ), separated by single spaces.
Each triple means that the tram can get from the junction number
), separated by single spaces.
Each triple means that the tram can get from the junction number 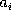 to junction
to junction 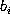 in
in 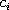 minutes.
All tracks are one-way, but it can happen that the trams can go both from junction
minutes.
All tracks are one-way, but it can happen that the trams can go both from junction 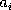 to
to 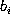 and from
and from 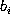 to
to 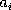 .
It can also happen that
.
It can also happen that 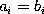 (a balloon loop).
There can be at most one connection in a given direction between a pair of junctions.
(a balloon loop).
There can be at most one connection in a given direction between a pair of junctions.
The time that the tram spends at a stop can be neglected. In addition, we assume that the tram goes as long is it can (until it reaches a dead end or infinitely long, if no dead end is ever reached by it).
Output
Output  integers to the standard output, each in a separate line.
The
integers to the standard output, each in a separate line.
The 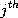 line should contain the number
line should contain the number 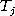 .
.
Example
For the input data:
7 8 1 2 1 2 3 4 3 2 4 4 6 3 6 5 3 3 3 2 5 4 4 5 7 1
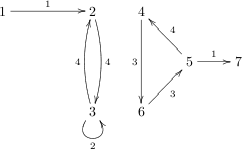
the correct result is:
-1 2 2 10 10 10 -1
Explanation of the example: A tram which leaves junction number 2 can return in, for example, 8, 10 or 12 minutes. Hence, for the camera not to miss any appearance of the tram, it should be set to make photos every two minutes.
Task author: Jakub Lacki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English